릿지 회귀

문제

혼공머신 03-3: 농어의 length, height, width 로 부터 농어의 weight 를 예측해 본다.

 

 

코드

Input 데이터 (농어의 length, height, width) 준비

import pandas as pd

df = pd.read_csv("https://bit.ly/perch_csv_data")
perch_full = df.to_numpy()
perch_full  # columns: length, height, width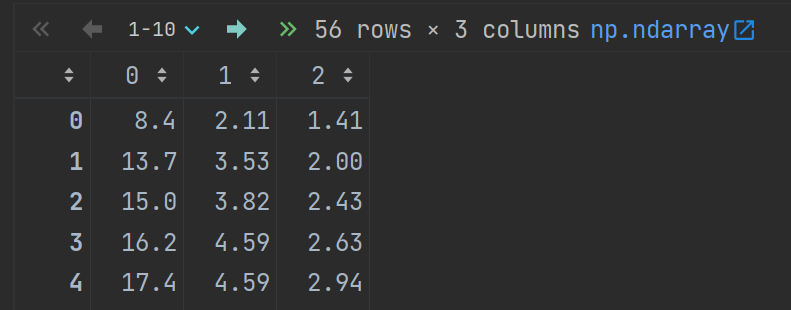

 

target 데이터 준비

import numpy as np

# 타깃 데이터: length, height, width 일 때, weight
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
                         115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
                         150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
                         218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
                         556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
                         850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
                         1000.0])

 

training 세트와 test 세트로 나누기

from sklearn.model_selection import train_test_split

train_input, test_input, train_target, test_target = train_test_split(
    perch_full, perch_weight, random_state=42
)

 

length, height, width 이외의 새로운 특성 추가

from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures(degree=5, include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)

train_poly.shape  # (42, 55): 특성의 개수가 55개!

 

데이터 정규화

from sklearn.preprocessing import StandardScaler

ss = StandardScaler()
ss.fit(train_poly)
train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)

 

모델 훈련

from sklearn.linear_model import Ridge

ridge = Ridge(alpha=1.0)  # default 1.0 사용
ridge.fit(train_scaled, train_target)
ridge.score(train_scaled, train_target)  # 0.9896101671037343
ridge.score(test_scaled, test_target)  # 0.9790693977615379

 

개선: 훈련에 사용할 최적의 alpha 값 찾기

앞의 훈련에서 alpha 값으로 default 1.0 을 사용했는데, 좀더 나은 alpha 값을 찾아보자.

alpha 값의 후보로 0.001, 0.01, 0.1, 1, 10, 100 을 선정하고 각각의 score 변화를 그래프로 확인해 보자.

그래프를 그릴때 scale 때문에 x 축을 np.log10() 으로 보정한다.

R^2 (결정계수): 회귀에서는 정확한 숫자를 맞히는 것이 거의 불가능하기 때문에 다른 방법으로 평가하는데 이 점수를 결정계수 (coefficient of determination) 라고 한다.

 

import matplotlib.pyplot as plt

train_score = []
test_score = []

alpha_list = [0.001, 0.01, 0.1, 10, 100]
for alpha in alpha_list:
    ridge = Ridge(alpha=alpha)

    ridge.fit(train_scaled, train_target)
    train_score.append(ridge.score(train_scaled, train_target))
    test_score.append(ridge.score(test_scaled, test_target))


plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)

plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show()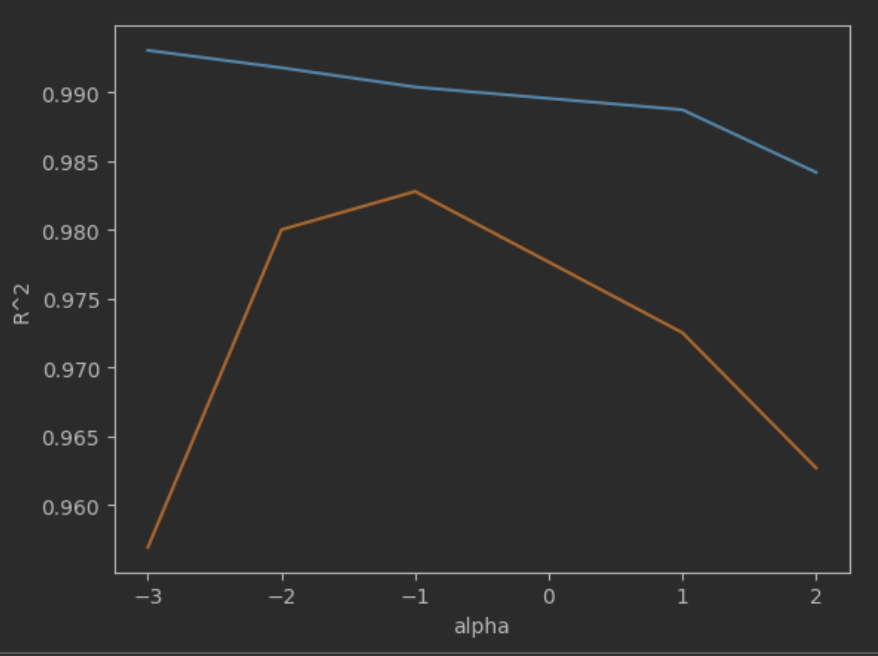

 

최적의 alpha 값 판단 후 해당 값으로 훈련

앞의 그래프를 봤을 때 -1 일 때, 즉 alpha=10^(-1)=0.1 일 때 R^2 값이 높은 것 같다.

alpha=0.1 로 훈련한다.

ridge = Ridge(alpha=0.1)

ridge.fit(train_scaled, train_target)
ridge.score(train_scaled, train_target)  # 0.9903815817570368
ridge.score(test_scaled, test_target)  # 0.9827976465386983

 

참고: 모델 coef 확인해 보기

앞서 특성을 55개 사용해서, coef 의 개수도 55개 이다.

ridge.coef_   # 55 rows x 1 columns
ridge.intercept_